Design of Counters - Example 1.5

Design of Counters

This example is taken from T. L. Floyd, Digital Fundamentals, Fourth Edition, Macmillan Publishing, 1990, p.395.

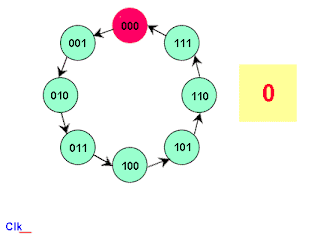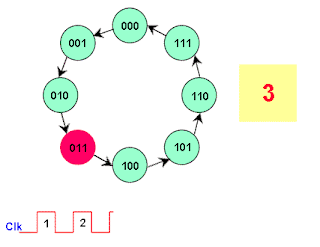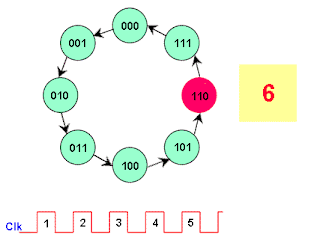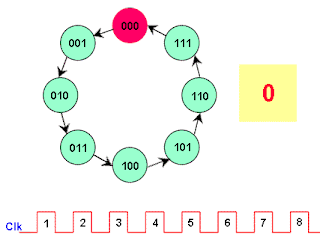
Example 1.5   A counter is first described by a state diagram, which is shows the sequence of states through which the counter advances when it is clocked. Figure 18 shows a state diagram of a 3-bit binary counter.

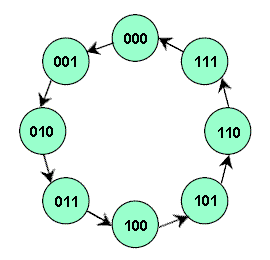Figure 18. State diagram of a 3-bit binary counter.

The circuit has no inputs other than the clock pulse and no outputs other than its internal state (outputs are taken off each flip-flop in the counter). The next state of the counter depends entirely on its present state, and the state transition occurs every time the clock pulse occurs. Figure 19 shows the sequences of count after each clock pulse.

Once the sequential circuit is defined by the state diagram, the next step is to obtain the next-state table, which is derived from the state diagram in Figure 18 and is shown in Table 15.

Table 15. State table

Present State Q2 Q1 Q0	Next State Q2 Q1 Q0
0   0   0 0   0   1 0   1   0 0   1   1 1   0   0 1   0   1 1   1   0 1   1   1	0   0   1 0   1   0 0   1   1 1   0   0 1   0   1 1   1   0 1   1   1 0   0   0

Since there are eight states, the number of flip-flops required would be three. Now we want to implement the counter design using JK flip-flops.

Next step is to develop an excitation table from the state table, which is shown in Table 16.

Table 16. Excitation table

Output State Transitions		Flip-flop inputs J2 K2 J1 K1 J0 K0
Present State Q2 Q1 Q0	Next State Q2 Q1 Q0
0  0  0 0  0  1 0  1  0 0  1  1 1  0  0 1  0  1 1  1  0 1  1  1	0  0  1 0  1  0 0  1  1 1  0  0 1  0  1 1  1  0 1  1  1 0  0  0	0 X 0 X 1 X 0 X 1 X X 1 0 X X 0 1 X 1 X X 1 X 1 X 0 0 X 1 X X 0 1 X X 1 X 0 X 0 1 X X 1 X 1 X 1

Now transfer the JK states of the flip-flop inputs from the excitation table to Karnaugh maps to derive a simplified Boolean expression for each flip-flop input. This is shown in Figure 20.

Figure 20. Karnaugh maps

The 1s in the Karnaugh maps of Figure 20 are grouped with "don't cares" and the following expressions for the J and K inputs of each flip-flop are obtained:

The final step is to implement the combinational logic from the equations and connect the flip-flops to form the sequential circuit. The complete logic of a 3-bit binary counter is shown in Figure 21.

Figure 21. Logic diagram of a 3-bit binary counter.

 

Example 1.6